Définition

Dans un espace vectoriel de dimension \(3\), on peut définir le produit vectoriel \(\vec u\land\vec v\) des vecteurs \(\vec u\) et \(\vec v\) comme étant le vecteur perpendiculaire au plan formé par \(\vec u\) et \(\vec v\) et dont la norme est égale à la surface du parallélogramme défini par ces mêmes vecteurs

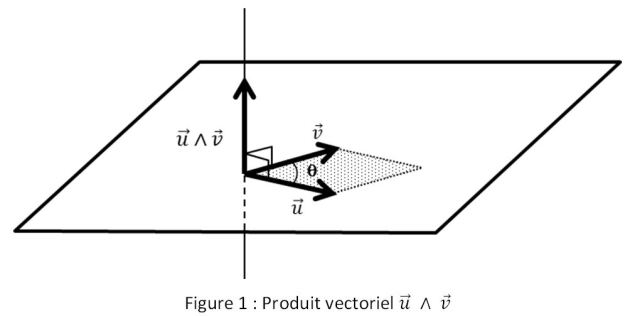On définit le produit vectoriel des deux vecteurs \(\vec u\) et \(\vec v\), noté \(\vec u\land\vec v\), comme étant le vecteur :

• normal au plan vectoriel de base \((\vec u,\vec v)\)
• dont la norme vaut \(\lVert\vec u\rVert\lVert\vec v\rVert\lvert\sin(\widehat{\vec u,\vec v})\rvert\)
• tel que \((\vec u,\vec v,(\vec u\land\vec v))\) forme une base directe

Notation

Notation : le produit vectoriel peut aussi être noté \(\vec u\times\vec v\) et \([\vec u,\vec v]\)

Propriétés

Propriétés du produit vectoriel :

• si \(\vec u\) et \(\vec v\) sont colinéaires, on a alors \({{\vec u\land\vec v}}={{0}}\)
• le produit vectoriel est antisymétrique : \({{\vec u\land\vec v}}={{-\vec v\land\vec u}}\)
• \(\vec u\), \(\vec v\) et \(\vec u\land\vec v\) forment un trièdre direct

Dans le plan, le produit vectoriel correspond au déterminant
(Plan, Déterminant)

Formules utiles

Formule générale du produit vectoriel

Calcul des composantes de \(\vec u\land\vec v\) selon les composantes de \(\vec u\) et \(\vec v\) : $$\vec u\begin{pmatrix}u_x\\ u_y\\ u_z\end{pmatrix}\qquad\vec v\begin{pmatrix}v_x\\ v_y\\ v_z\end{pmatrix}$$$\(\vec u\land\vec v\begin{pmatrix}{{u_yv_z-u_zv_y}}\\ {{u_zv_x-u_xv_z}}\\ {{u_xv_y-u_yv_x}}\end{pmatrix}\)$
Soient \(\vec u\begin{pmatrix}a_1\\ a_2\\ a_3\end{pmatrix}\) et \(\vec v\begin{pmatrix}b_1\\ b_2\\ b_3\end{pmatrix}\) deux vecteurs. $${{\vec u\land\vec v}}={{\vec i\begin{vmatrix}a_2&b_2\\ a_3&b_3\end{vmatrix}-\vec j\begin{vmatrix}a_1&b_1\\ a_3&b_3\end{vmatrix}+\vec k\begin{vmatrix}a_1&b_1\\ a_2&b_2\end{vmatrix} }}$$

Dérivée

$$\left({{\vec u\land\vec v}}\right)'={{\vec u'\land\vec v+\vec u\land\vec v'}}$$

Produits vectoriels particuliers

Vecteurs unitaires

Avec les vecteur unitaire : $$\vec i\land\vec j={{\vec k}}$$
(Vecteur unitaire - Vecteur unité)

Vecteur nul

Avec vecteur nul : $$\vec u\land{{\vec0}}={{\vec 0}}$$
(Vecteur nul)

Antisymétrie

Antisymétie du produit vectoriel : $$\vec u\land\vec v=-\vec v\land\vec u$$
(Fonction antisymétrique - Fonction anti-symétrique)

Produit vectoriel par soi-même

$$\vec u\land\vec u={{\vec 0}}$$

Homogénéité

$$(\lambda\vec u)\land v={{\lambda(\vec u\land\vec v)}}$$
(Homogénéité - Fonction homogène)

Additivité

Additivité du produit vectoriel : $$(\vec u_1+\vec u_2)\land\vec v={{\vec u_1\land\vec v+\vec u_2\land\vec v}}$$
(Additivité - Fonction additive)

Vecteurs colinéaires

Deux vecteurs \(\vec u\) et \(\vec v\) sont colinéaires si $${{\vec u\land\vec v}}={{0}}$$
(Vecteurs colinéaires - Colinéarité)